TA32钛合金板材的超塑胀形性能研究

钛合金具有良好的高温综合性能，抗疲劳、抗氧化和耐腐蚀性能优异，被广泛用于制备航空航天、船舶等领域中的关键构件[1]。但由于钛合金在室温下存在成形抗力大、塑性差和回弹大等问题，常采用热加工技术进行制造。武永等[2] 综述了多种针对钛合金薄壁构件的热成形工艺，其中超塑气胀成形技术是近年来发展起来的一种先进工艺方法，具有成形效率高、适用性强、绿色环保等优点，可将简单形状坯料直接成形为整体复杂曲面零件。Li 等[3] 研究了超塑胀形过程中摩擦系数、应变速率敏感系数和应变速率等对板料厚度分布的影响。Alabort 等[4] 基于黏塑性模型预测了TC4钛合金多层板在超塑气胀成形过程中几何形状、应变分布、晶粒尺寸和损伤分数的演变规律。Fan 等[5] 通过开展超塑气胀成形试验发现，在热成形过程中，不同的应变路径会显著影响钛合金的微观组织、织构演变及变形机制，进而改变宏观力学性能及成形零件质量。此外，Li[6]和 Wu[7] 等通过高温单轴拉伸试验发现近 α 钛合金板材由于具有强烈的轧制织构，在高温塑性变形时仍然表现出明显的各向异性。因此，有必要对不同双拉应变路径下钛合金板材的高温力学性能及各向异性行为进行系统研究，这对于优化成形工艺和提高有限元精度具有重要的指导意义。

TA32钛合金是中科院金属研究所在 Ti55合金基础上改进的一种近α型高温钛合金，已被用于研制国内先进航空发动机的加力燃烧室筒体和尾喷管结构件[8]。

本文通过开展高温气胀成形试验研究了TA32钛合金板材的超塑胀形性能。设计了4种具有不同短长轴比的椭圆模具以实现不同的应变路径，板材的轧向 （Rolling direction，RD）和横向 （Transverse direction，TD）分别与模具长轴平行以研究变形各向异性。分析了胀形试样顶点的应变分量、壁厚和曲率半径与胀形高度之间的定量关系。基于非关联流动法则下的 Barlat’89 屈服准则对 TA32板材胀形过程中的等效应力进行了求解，并分析了不同应变路径下试样顶点处的等效应力-应变曲线和等效应变速率。

1、 超塑胀形性能试验

试验材料为宝钛集团生产的0.8mm厚近α型TA32钛合金轧板，名义成分为 Ti-5.5Al-3.5Sn-3.0Zr-0.7Mo -0.3Si-0.4Nb-0.4Ta（质量分数，%）[8]。通过激光切割制备直径为 90 mm 的圆形试样，并用砂纸打磨试样表面去除边缘毛刺。为了测量胀形试样的应变分布，采用电蚀刻打标机在试样表面印制线宽0.02mm×边长 2mm的方形网格。

在自主设计的成形装置上对 TA32钛合金薄板进行超塑气胀成形试验，装置示意如图 1 所示。首先通过加热炉将上、下模具加热至成形温度 （800 ℃），采用 3 个K 型热电偶实时监测上模座、模具和下模座的温度。然后，将涂有高温防氧化剂的圆形试样 （直径 90 mm）置于模具之间，保温 15 min 后通过夹紧模具来密封腔体。

将高压气体从下模座中的孔道沿指定加载曲线施加于试样的下表面，使其发生塑性变形。同时，在下模座型腔中放置了大量陶瓷球，一方面减小板料中部和板料与模具接触区域之间的温度差异，另一方面降低低温高压气体对试样表面的温降影响。在试验过程中，胀形高度由位移传感器实时监测，加载气压由电动比例调节阀控制，并通过压力传感器实时记录。

为了研究不同应变路径下的胀形性能，设计了 4 套具有不同椭圆型腔结构的模具，如图 2（a）~（d）所示。

模具长轴平行于 X 轴，短轴平行于 Y 轴。变形区域的长轴为 60 mm，短长轴比用 λ 表示，4 套模具的短长轴比分别为 1、3/4、2/4 和 1/4。不同模具代表的双轴拉伸应变路径的示意图见图 2（e），分别标记为路径 1~4。为了分析 TA32 板材在超塑胀形条件下的各向异性行为，在胀形过程中使得试样的 RD 和 TD 分别平行于模具的长轴 （X 轴）方向。

采用 Banabic[9] 和 Siegert[10] 等提出的气压加载方程，使得试样顶点在胀形过程中保持恒定等效应变率变形。

式中，p为胀形压力；a0 和 b0 分别为模具型腔的半长轴和半短轴长度；s0 为初始板厚；t 为胀形时间；α 为主应力比值的无量纲常数；ε.e 为等效应变速率；σ- 为对应于单轴拉伸期间特定应变速率的等效流动应力。根据本课题组之前的研究结果[11]，TA32 板材在 800 ℃下以0.001 s^–1 应变速率变形时表现出良好的超塑性，因此本文设定试样顶点在胀形过程中的等效应变速率为 0.001s^–1，相应的等效流动应力约为 120 MPa。图 3 为 TA32板材在不同应变路径下的胀形压力加载曲线。可以看出，恒应变速率胀形气压先快速增加后缓慢减小，气压减小的原因是由于板料发生了局部软化。同时，随着模具短长轴比的减小，胀形压力显著增加。

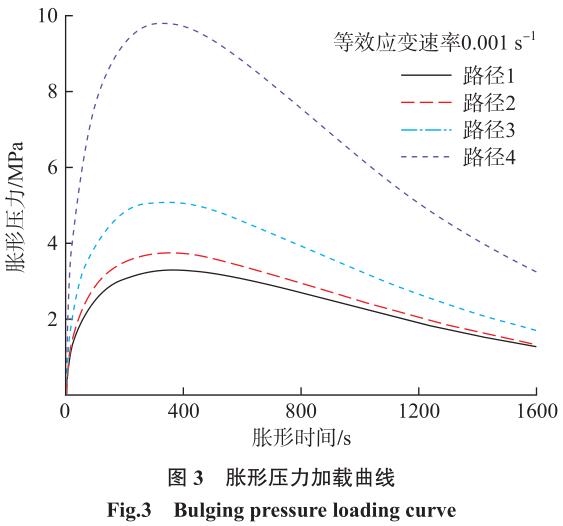
2、 胀形过程分析模型

由于板厚与模具直径之比小于 0.02，采用薄膜理论分析胀形试样顶点应力[12]。为简化计算，提出以下近似假设： （1）法向应力和弯曲应力等于 0； （2）壁厚分布均匀； （3）在两个正交方向上的应力分量是均匀的，且垂直于相应截面； （4）外表面曲率半径在微元体范围内均匀分布，根据法向方向的力平衡方程，试样顶点处的应力分量可表示为[13]

式中，s 为试样顶点的当前壁厚；ρX 和 ρY 为试样外表面沿 X 和 Y 轴的曲率半径。

等效应力通过合适的屈服准则转化主应力来获得，本文选取适用于各向异性金属板的 Barlat’89 屈服准则来描述 TA32 板材的屈服行为[14]。为了使等效应力预测结果更加准确，采用非关联流动法则下的 Barlat’89屈服准则进行求解，在平面应力状态下可表示为[15]

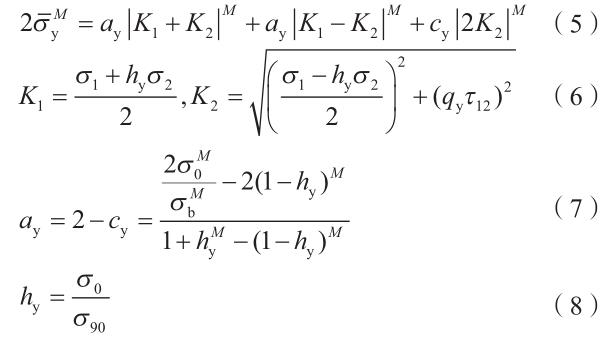
式中，σ- 为等效应力；上标 M 为幂指数；K1、K2 为方程参数；σ1、σ2 为第 1 和第 2 主应力；τ 为剪切应力；ay、cy 和hy 为材料参数；考虑到在胀形过程中试样顶点的剪应力接近于 0，故参数 qy 可忽略不计；σ0 和 σ90 分别为 TA32板材平行 RD 和垂直 RD 单轴拉伸时的屈服应力[16] ；σb为等双拉时的屈服应力，可近似表示为 σb =（σ0 + σ90）/2。

表 1 列出了非关联流动法则下 Barlat’89 屈服准则中的材料参数。

利用塑性功相等原则计算等效应变增量[17] 为

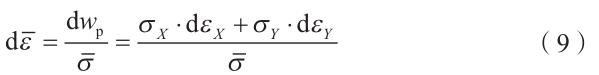
式中，wp 是单位体积内的塑性功增量；dεX 和 dεY 是沿 X和 Y 轴的应变增量。等效应变可通过对增量积分得到。

由式 （3）可知，应力分量的求解依赖于试样顶点的主曲率半径 （ρX、ρY）。在本研究中，假设胀形试样的长轴截面轮廓近似为圆形，通过考虑模具圆角半径的影响，试样顶点处沿长轴的曲率半径可表示为[18]

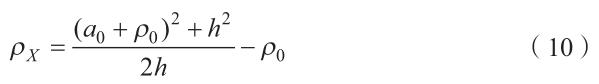
式中，ρ0 为模具圆角半径；h 为胀形高度。

根据 Chen[19] 的研究结果，胀形试样主曲率半径之比与模具短长轴比之间的关系可表示为

式中，参数 c1 用于反映材料的各向异性，由路径 1 下胀形试样的主曲率半径之比得到；参数 c2 为不同应变路径对曲率半径的影响因子，通过拟合路径 2~ 4 下胀形试样的主曲率半径得到。

3 、结果与讨论

图 4 为 TA32 板材在 800 ℃下沿不同应变路径胀形至不同阶段的试验结果。试样轧向与模具长轴方向平行。图 5 为不同路径下试样顶点处的胀形高度与时间之间的关系。可以看出胀形高度在变形初期迅速增加，增长速率随着变形的发展而逐渐减慢。当变形到最后阶段时，胀形高度在短时间内迅速增加，直到试样破裂。

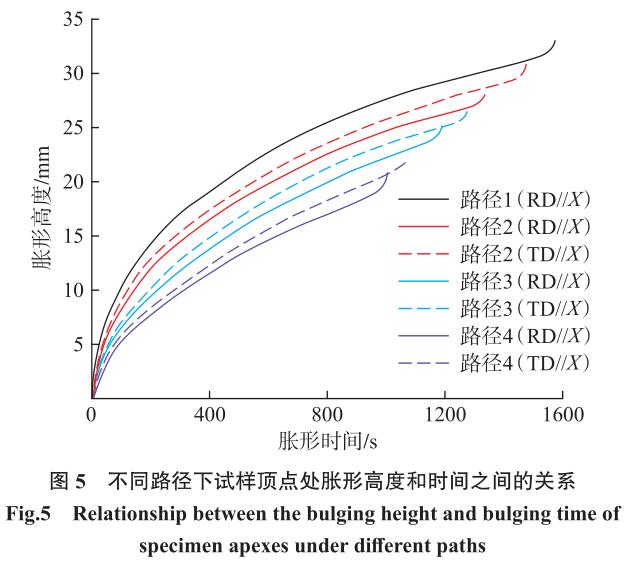
同时，胀形高度随模具短长轴比的减小而减小。当试样 RD 平行于 X 轴时，路径 1~ 4 的极限胀形高度分别为33.1 mm、28.1 mm、25.3 mm 和 20.4 mm；当试样 TD 平行于 X 轴时，路径 2~4 的极限胀形高度分别为 30.8mm、26.9mm 和 22.2mm，这表明 TA32 板材在高温胀形试验中具有明显的变形各向异性。

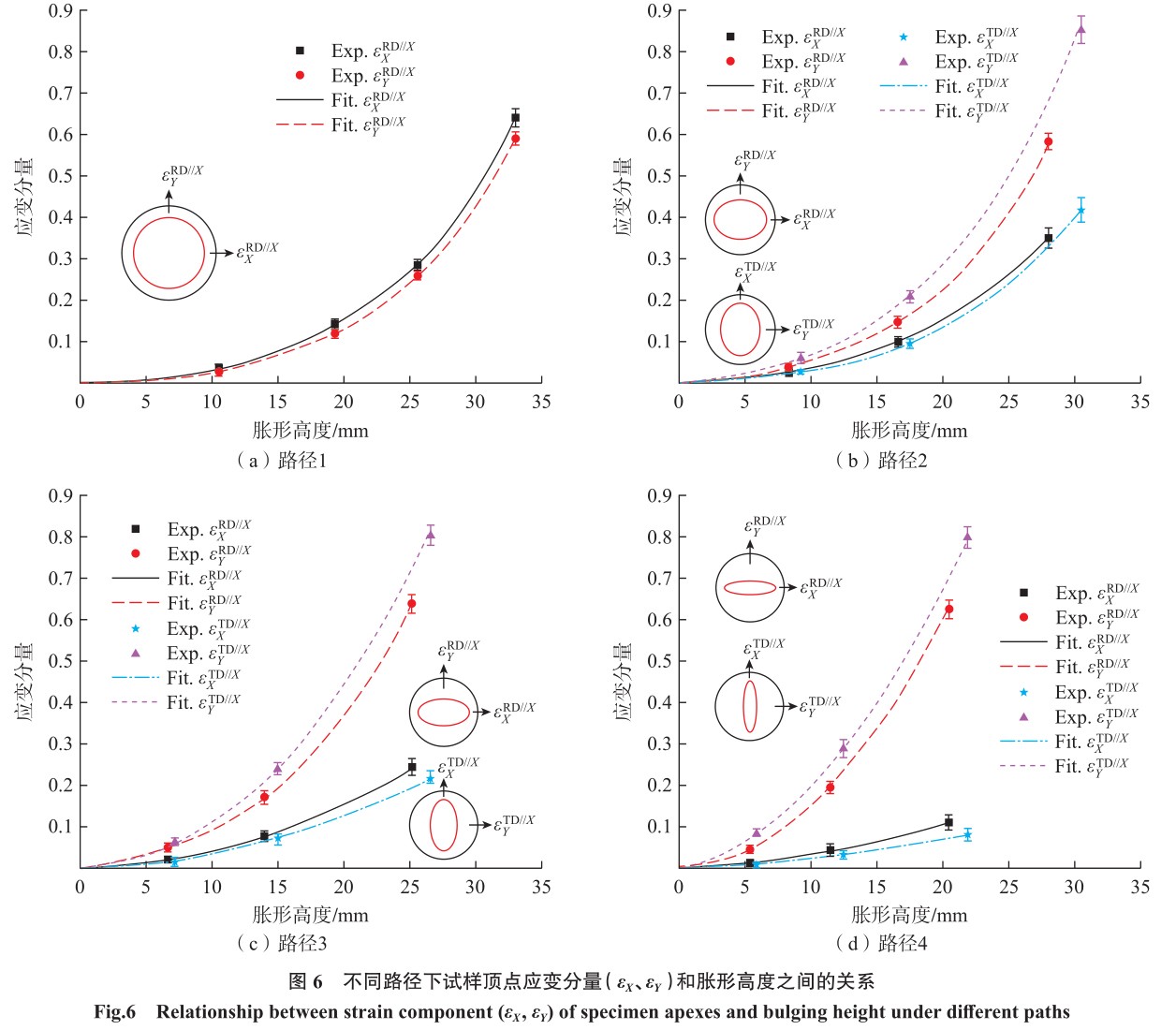
通过测量胀形试样顶点区域变形网格的应变分布，得到了不同应变路径下试样顶点处应变分量 （εX、εY）和胀形高度之间的对应关系，并用二次多项式对其进行拟合，如图 6 所示 （上标“RD//X ”和“TD//X ”表示两个不同的试样，下标“X ”和“Y ”表示应变分量对应的方向）。

随着胀形高度的增加，应变增量逐渐增大。当使用圆形模具胀形时，短轴方向上应变略小于长轴方向上应变；当使用椭圆模具胀形时，短轴方向上应变大于长轴方向上应变，且差值随模具短长轴比的减小而增加。此外，与 RD//X 试样相比，在相同胀形高度下，TD//X 试样在短轴方向上的应变更大，而在长轴方向上的应变更小。

这种各向异性行为可能与原始轧板中的织构分布密切相关[7]。图 7[7] 显示了由 Channel 5 软件绘制的 TA32钛合金板材的 （0001）、（101-0）和 （112-0）极图，可以看出，原始板材中存在着大量的横向织构（Transverse），即图 7 中 T 所在位置。

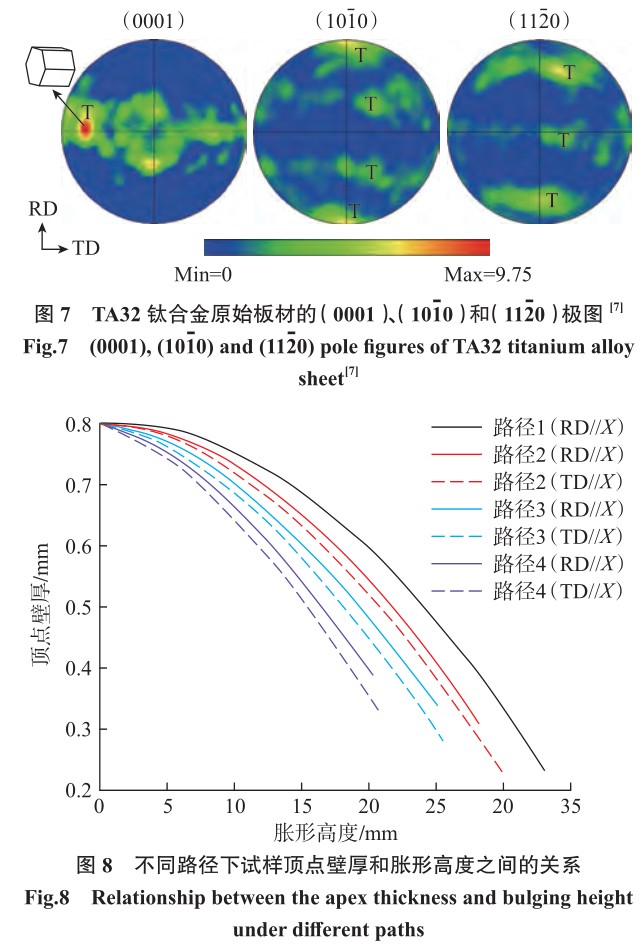
根据材料不可压缩假设，进一步得到不同应变路径下试样顶点壁厚和胀形高度之间的关系，如图 8 所示。

试样减薄率随着胀形高度的增加而快速增加，且随着模具 λ 值的减小，试样壁厚在相同胀形高度下明显减小。

同时，与 RD//X 试样相比，TD//X 试样在相同变形条件下具有更大的变形能力，表明当 RD 平行于第一主应变方向时，TA32 板材在高温双拉条件下表现出更好的塑性。

图 9 显示了不同应变路径下试样顶点曲率半径和胀形高度之间的关系（其中符号点表示试验值），通过采用高度尺分别构建胀形试样沿 X 和 Y 轴的截面轮廓，并拟合二次曲线方程获得。结合式 （11），c1 和 c2 的数值分别为 1.07 和 1.15，理论计算的曲率半径如图 8 所示。可以看出预测结果与试验结果吻合较好。随着胀形高度的增加，试样顶点曲率半径先快速降低后缓慢降低，且在短轴方向上减小速度更快。随着变形的进行，短轴方向上的曲率半径逐渐趋近于模具的半短轴长度。随着模具 λ 值的减小，沿长轴方向的曲率半径接近，但沿短轴方向的曲率半径不断减小。此外，当使用同一套模具胀形至相同高度时，RD//X 和 TD//X 试样的曲率半径几乎相同，这意味着曲率半径主要取决于模具型腔结构，与板材取向无关。

根据上文的分析，基于 Barlat’89 屈服准则 （式 （5））并结合上述试验数据计算了不同应变路径下试样顶点处的等效应力 – 应变曲线，如图 10 所示。可以看出流动应力在变形初期迅速达到峰值，随后由于动态再结晶和损伤积累而逐渐下降，表现出明显的流变软化行为。随模具 λ值的减小，即路径 1~ 4，材料的峰值应力升高，流变软化增强，延伸率降低，表明当应变路径由等双拉过渡到平面应变时，材料的成形性能不断下降。另外，力学性能表现出明显的各向异性，当板材 TD 与模具长轴平行时，材料具有更低的峰值强度和更高的塑性，即当板材 RD 与第一主应变方向平行时，TA32 板材具有更好的成形性。

式 （6）计算了试样顶点在不同应变路径下胀形时的等效应变速率，如图 11 所示，可以发现在胀形过程中应变速率主要分为3个阶段：快速下降、稳定波动和加速上升。

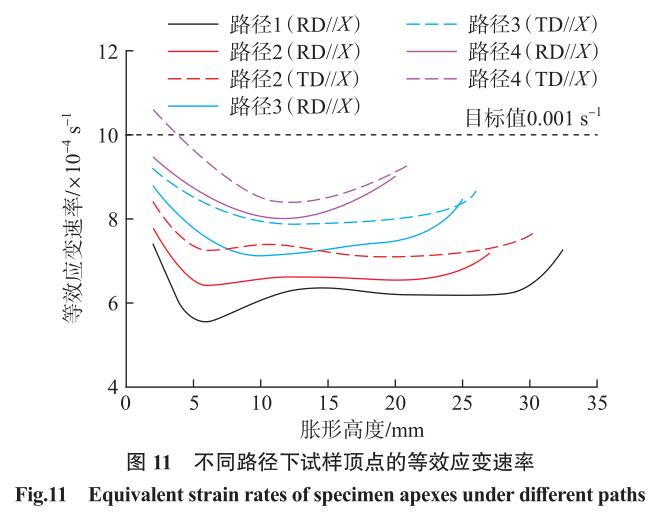
但是，不同路径下的应变速率均低于目标设定值，这意味着通过式 （1）计算得到的压力加载曲线无法满足 TA32板材的恒应变速率胀形，未来需要开发适用性更强的理论模型来准确预测超塑气胀成形过程中的加载压力。

4、 结论

（1）TA32钛合金板材的超塑气胀成形性能表现出强烈的应变路径依赖性。当应变路径从等双轴拉伸转变为近平面应变时，板材极限胀形高度减小，峰值应力增加，延伸率降低，成形性能下降。

（2）TA32钛合金板材在超塑成形条件下表现出显著的各向异性行为。当板材 RD 平行于第一主应变方向时，材料具有更低的峰值应力和更高的塑性，表现出更好的成形性。

参 考 文 献

[1] YUAN S J. Fundamentals and processes of fluid pressure forming technology for complex thin-walled components[J]. Engineering,2021, 7(3): 358–366.

[2] 武永 , 陈明和 . 钛合金薄壁件热塑性成形工艺研究进展 [J].航空制造技术 , 2021, 64(20): 78–87.

WU Yong, CHEN Minghe. Progress of hot metal plastic forming technology for titanium alloy thin-walled parts[J]. Aeronautical Manufacturing Technology, 2021, 64(20): 78–87.

[3] LI G Y, TAN M J, LIEW K M. Three-dimensional modeling and simulation of superplastic forming[J]. Journal of Materials Processing Technology, 2004, 150(1–2): 76–83.

[4] ALABORT E, PUTMAN D, REED R C. Superplasticity in Ti–6Al–4V: Characterisation, modelling and applications[J]. Acta Materialia,2015, 95: 428–442.

[5] FAN R L, WU Y, CHEN M H, et al. Analysis of texture evolution and slip activity of a near-α titanium alloy sheet under different biaxial-tension strain paths[J]. Journal of Materials Research and Technology, 2022, 20: 2905–2920.

[6] LI W Y, CHEN Z Y, LIU J R, et al. Effect of texture on anisotropy at 600 ℃ in a near-α titanium alloy Ti60 plate[J]. MaterialsScience and Engineering: A, 2017, 688: 322–329.

[7] WU Y, FAN R L, CHEN M H, et al. High-temperature anisotropic behaviors and microstructure evolution mechanisms of a near-α Ti–alloy sheet[J]. Materials Science and Engineering: A, 2021, 820: 141560.

[8] 王清江 , 刘建荣 , 杨锐 . 高温钛合金的现状与前景 [J]. 航空材料学报 , 2014, 34(4): 1–26.

WANG Qingjiang, LIU Jianrong, YANG Rui. High temperature titanium alloys: Status and perspective[J]. Journal of Aeronautical Materials,2014, 34(4): 1–26.

[9] BANABIC D, VULCAN M, SIEGERT K. Bulge testing under constant and variable strain rates of superplastic aluminium alloys[J].CIRP Annals, 2005, 54(1): 205–208.

[10] SIEGERT K, JÄGER S, VULCAN M. Pneumatic bulging ofmagnesium AZ 31 sheet metals at elevated temperatures[J]. CIRP Annals,2003, 52(1): 241–244.

[11] WU Y, FAN R L, QIN Z H, et al. Shape controlling and property optimization of TA32 titanium alloy thin-walled part prepared by hot forming[J]. Transactions of Nonferrous Metals Society of China,2021, 31(8): 2336–2357.

[12] REIS L C, OLIVEIRA M C, SANTOS A D, et al. On the determination of the work hardening curve using the bulge test[J]. International Journal of Mechanical Sciences, 2016, 105: 158–181.

[13] HE Z B, ZHU H H, LIN Y L, et al. A novel test method for continuous nonlinear biaxial tensile deformation of sheet metals by bulging with stepped-dies[J]. International Journal of Mechanical Sciences, 2020, 169: 105321.

[14] BARLAT F, LIAN K. Plastic behavior and stretchability of sheet metals. Part I: A yield function for orthotropic sheets under plane stress conditions[J]. International Journal of Plasticity, 1989, 5(1): 51–66.

[15] MIN J Y, CARSLEY J E, LIN J P, et al. A non-quadratic constitutive model under non-associated flow rule of sheet metals with anisotropic hardening: Modeling and experimental validation[J]. International Journal of Mechanical Sciences, 2016, 119: 343–359.

[16] FAN R L, WU Y, CHEN M H, et al. Prediction of anisotropic deformation behavior of TA32 titanium alloy sheet during hot tension by crystal plasticity finite element model[J]. Materials Science and Engineering:A, 2022, 843: 143137.

[17] REIS L C, PRATES P A, OLIVEIRA M C, et al. Anisotropy and plastic flow in the circular bulge test[J]. International Journal of Mechanical Sciences, 2017, 128–129: 70–93.

[18] AKSENOV S, SORGENTE D. Determination of biaxial stress–strain curves for superplastic materials by means of bulge forming tests at constant stress[J]. CIRP Journal of Manufacturing Science and Technology, 2020, 31: 618–627.

[19] CHEN K. A general and unified theory of the kinematic relationships in bulge tests[J]. Journal of the Mechanics and Physics of Solids, 2020, 143:104086.

通讯作者：武永，副教授，工学博士，研究方向为钛合金超塑成形 / 扩散连接工艺及装备、高温成形多尺度建模。